5.Klasse: Funktionen / 3 von 7 weiter zurück
Lineare Funktionen
- Eine Funktion f mit Funktionsterm y = f(x) = k.x (k ∈ R) heißt homogene lineare Funktion.
Dabei heißt k die Steigung der homogenen linearen Funktion.
- Der Graph einer homogenen linearen Funktion ist eine Gerade, die durch den Ursprung geht.
Ist k > 0 steigt die Gerade, ist k < 0 fällt die Gerade.
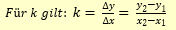
- Eine Funktion f mit Funktionsterm y = f(x) = k.x + d (k,d ∈ R, d ≠ 0) heißt inhomogene lineare Funktion.
Auch hier heißt k die Steigung der inhomogenen linearen Funktion, d gibt den Abstand des Schnittpunktes des Funktionsgraphen mit der y-Achse vom Ursprung an.
- Der Graph einer inhomogenen linearen Funktion ist eine Gerade, die nicht durch den Ursprung geht.