7.Klasse: Kurvendiskussion / 4 von 4 weiter zurück

Graphisches Differenzieren (anhand einer Polynomfunktion)

Für das graphische Differenzieren f(x) ➔ f'(x) gilt
grundsätzlich:
  • Wendepunkt (WP) wird Extremwert,
  • Extremwert (EW) wird Nullstelle,
    Sattelpunkt (SP) wird Nullstelle,
  • Nullstelle (NS) wird zu Punkt
    - oberhalb der x-Achse,
       wenn NS-Tangente pos. Anstieg hat,
    - unterhalb der x-Achse,
       wenn NS-Tangente neg. Anstieg hat.


    • Beachte:
    Das graphische Differenzieren ergibt nur einen
    ungefähren Graphen der Ableitungsfunktion,
    keine exakte Darstellung wie bei der Berechnung.

    Vorgehensweise:

    1.Schritt: NS in Ableitung unterhalb EW markieren

    2.Schritt: weitere Punkte in Ableitung positionieren:
  • je nach Anstieg der NS-Tangente im positiven oder negativen Bereich;
  • der WP ergibt MAX, wenn WP-Tangente pos. Anstieg hat, sonst MIN
    • ➔ ungefährer Verlauf der Ableitung

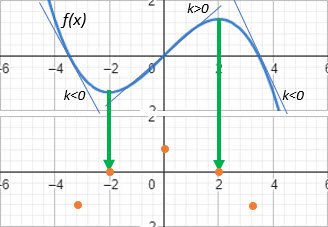
    		 xxxxx
    Home | Kontakt | Haftungsausschluss | Impressum | Datenschutzerklärung
    [© Dipl.Ing. Bernhard Schleser] / V 1.0