8.Klasse: Kegelschnitte / 3 von 4 weiter zurück
Hyperbel (in 1.Hauptlage)
Die Hyperbel ist die Menge aller Punkte, für die gilt: Differenz der Abstände zu den zwei Brennpunkten ist konstant (= 2a).
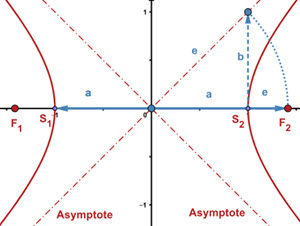
| Gleichung Hyperbel | b2 x2 - a2 y2 = a2 b2 | a, b: Hauptachsen; | |
| Gleichung Tangente | b2 x x1 - a2 y y1 = a2 b2 | x1, y1: Koordinaten eines Punktes auf der Hyperbel | |
| Berührbedingung | a2 k2 - b2 = d2 | k, d: Werte aus Tangentengleichung (Gerade) | |
| Gleichung Assymptoten | y = (b / a) * x | bzw. y = -(b / a) * x | |
| Es gilt | e2 = a2 + b2 | e: lineare Exzentrizität, Abstand M zu Brennpunkten F1, F2 |