8.Klasse: Wahrscheinlichkeit / 2 von 6 weiter zurück
Bei der Binomialverteilung werden diskrete Zufallsvariable betrachtet, die nur ganzzahlige positive Werte annehmen können, also X = 0, 1, 2, ., n.
Bei vielen Betrachtungen ist es aber sinnvoll, dass die Zufallsvariable beliebige reelle Werte annehmen kann, z.B.: Brenndauer einer Kerze, Länge eines Nagels, Kopfumfang eines Neugeborenen, etc.
Normalverteilung
Bei der Normalverteilung werden stetige Zufallsvariable betrachtet, die beliebige Zahlenwerte aus dem Bereich der reellen Zahlen annehmen können.
Definition
Eine stetige Zufallsvariable X heißt normalverteilt mit dem Erwartungswert μ und der Standardabweichung σ [kürzer: X ist N(μ;σ)-verteilt],
wenn die Wahrscheinlichkeit, dass X einen Wert zwischen x1 und x2 annimmt, folgendermaßen bestimmt ist:
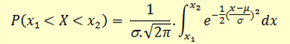
Dichtefunktion
Die Funktion